Dos triángulos son semejantes si tienen la misma forma pero no el mismo
tamaño, para indicar que dos triángulos son semejantes se utiliza el símbolo~.
Donde el símbolo ~ se lee "es semejante"
Ejemplo:
Para indicar que dos triángulos son semejantes se expresa de la siguiente manera:
ΔABC~ΔA´B´C´
PROPIEDADES FUNDAMENTALES DE LOS TRIÁNGULOS
SEMEJANTES
Propiedad I:
Dos triángulos son semejantes si sus ángulos correspondientes son
iguales, ejemplo:
ΔABC~ΔA´B´C´
porque los ángulos son los siguientes:
ÐA=ÐA´
ÐB=ÐB´
ÐC=ÐC´
Ejemplo:
Propiedad II:
Dos triángulos son semejantes si la razón (comparación entre dos lados) es proporcional.
Ejemplo:
TEOREMAS DE SEMEJANZA DE TRIÁNGULOS
Teorema I:
Dos triángulos son semejantes si tienen dos ángulos homólogos, es decir
iguales, en este caso el teorema solo requiere dos ángulos mientras que la
propiedad menciona todos.
Ejemplo:
Si <C=<C´ y <A=A´, entonces, el Δ ABC~ Δ A´B´C´
Teorema II:
Dos triángulos son semejantes si sus tres lados son proporcionales, en
este caso el teorema menciona los tres lados mientras que la propiedad solo
requiere la razón, lo que quiere decir que es la comparación entre dos lados
del triángulo.
Ejemplo:
por lo tanto Δ ABC~ Δ A´B´C´
Teorema III:
Dos triángulos son semejantes si
tienen un ángulo igual y los lados que forman dicho ángulo son proporcionales.
Ejemplo:


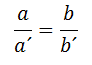






No hay comentarios:
Publicar un comentario