RELACIÓN ENTRE GRADOS Y RADIANES
RADIÁN:
Es la medida de un ángulo, donde el vértice de origen se
encuentra en el punto medio de una circunferencia, cuyo arco tiene la misma
longitud que el radio.
Ejemplo:
La forma para calcular la longitud del arco de una circunferencia es:
s= rq
s= longitud del arco
r= radio
q= amplitud del ángulo
CONVERSIÓN DE GRADOS
A RADIANES
La fórmula general utilizada para la conversión de grados a
radianes o también conocido como la conversión del Sistema Sexagesimal a Sistema Cíclico
es:
Ejemplo 1
(Convertir 50° a rad):
Primero se multiplican los grados a convertir por ambos
lados de la fórmula para que se pueda representar una igualdad en la fórmula
original.
Posteriormente se realiza la multiplicación del lado
izquierdo, en este caso se multiplica 50 x 1°;por otra parte se divide el valor
de pi (π) entre 180, quedando de esta forma:
50°= (0.0174) (50) rad
Después, el resultado de la división de π entre 180 se
multiplica por los grados a convertir (50):
50°=0.87 rad
Así de esa forma se obtiene el valor de 50° en rad.
Para entender he aquí otro ejemplo…
Ejemplo 2
(Convertir 130° a rad):
Primero se multiplican los grados a convertir por ambos
lados de la fórmula para que se pueda representar una igualdad en la fórmula
original.
Posteriormente se realiza la multiplicación del lado
izquierdo, en este caso se multiplica 130 x 1°;por otra parte se divide el
valor de pi (π) entre 180, quedando de esta forma:
130°= (0.0174) (130) rad
Después, el resultado de la división de π entre 180 se
multiplica por los grados a convertir (130):
130°=2.262 rad
Así de esa forma se obtiene el valor de 130° en rad.
CONVERSIÓN DE RADIANES
A GRADOS
La fórmula general utilizada para la conversión de radianes
a grados o también conocido como la conversión del Sistema Cíclico a Sistema Sexagesimal es:
Ejemplo 1
(convertir 2π rad= ¿? Grados):
Del mismo modo que la conversión de grados a radianes,
Primero se multiplican el rad a convertir por ambos lados de la fórmula para
que se pueda representar una igualdad en la fórmula original.
Posteriormente se realiza la multiplicación del lado
izquierdo, en este caso 2π x rad; por otra parte 2π sustituye al 180 de modo
que 2π se divida entre π y el resultado se multiplique por 180, quedando de la
siguiente manera:
El resultado queda de la siguiente manera, pues π al
dividirse entre π se cancela:
2π rad = 2 (180)
Después, el 2 se multiplica con el 180, teniendo como
resultado lo siguiente:
2π rad = 360°
Ejemplo 2
(Convertir 5π rad = ¿? Grados)
Del mismo modo que la conversión de grados a radianes,
Primero se multiplican el rad a convertir por ambos lados de la fórmula para
que se pueda representar una igualdad en la fórmula original.
Posteriormente se realiza la multiplicación del lado
izquierdo, en este caso 5π x rad; por otra parte 5π sustituye al 180 de modo
que 5π se divida entre π y el resultado se multiplique por 180, quedando de la
siguiente manera:
El resultado queda de la siguiente manera, pues π al
dividirse entre π se cancela:
5π rad = 5 (180)
Después, se multiplica 5 por el 180, teniendo como
resultado:
5π rad = 900°


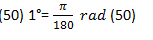






No hay comentarios:
Publicar un comentario