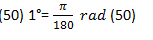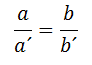COEVALUACION
ANA KAREN CONTRERAS ESCOBAR CALIF. 10
JAQUELINE BASILIO GONZÁLEZ CALIF. 10
sábado, 11 de octubre de 2014
domingo, 5 de octubre de 2014
CONVERSIÓN DEL SISTEMA SEXAGÉSIMAL AL SISTEMA DECIMAL Y VICEVERSA
MEDIDA DE ÁNGULOS Y SISTEMAS PARA MEDIRLOS
A) DECIMAL
Es de base 10, utiliza como símbolo el punto (.) y como supraíndice °
(indica grados)
B) SEXAGÉSIMAL
Es de base 60, utiliza como símbolo el grado (°), minuto (´) y segundo
(´´)
C) CÍCLICO
Es en base al radian, utiliza a π con valores expresados en
relación a π
RADIAN
Un radian es cuando el radio y la longitud del circulo miden lo
mismo
Ejemplo 1:
Convierte 20° 30´ al sistema decimal
Para hacer la conversión del Sistema Sexagésimal al Sistema Decimal
se siguen los siguientes pasos:
1.Los grados se van a pasar como enteros -----> 20.0
2. Para convertir los 30´ se divide 30/60 que son los minutos que
contiene una hora
Como resultado obtenemos .5 -----> 30´=.5
Y para finalizar subimos el .5 a los enteros, como resultado tenemos
que:
20° 30´ = 20.5
Ejemplo 2:
Convierte 347° 54´37´´ al sistema decimal
1. Los grados se pasan a enteros ------> 347.0
2. Para convertir los 54´ se divide 54/60 que son los minutos que tiene
una hora
Como resultado obtenemos .9 -----> 54´ =
.9
3. Se convierten los 37´´, se divide 37/60 que son los minutos que
conforman una hora
Como resultado obtenemos .6 -----> 37´´ =
.6
Pero como apenas hemos llegado a minutos y lo que queremos obtener son
segundos se repite el procedimiento
El .6 de divide entre 60 que son los segundos que conforman un minuto,
lo que da como resultado ---> 0.01
Y para finalizar subimos los minutos y los segundos que hemos obtenido a
los enteros obteniendo que:
347° 54´37´´ = 347.91
Para hacer la conversión del Sistema Decimal al Sistema Sexagésimal
se hace un procedimiento parecido al anterior solo que ahora se multiplicara
Ejemplo 1:
Convierte 25.5 al sistema sexagésimal
Pasos:
1. Los enteros se pasan a grados directamente --------> 25°
2. Para convertir el .5 a minutos se multiplica por 60 que son los
minutos que conforman una hora
Se obtiene que: .5*60 = 30´
Para finalizar se suben los minutos que hemos obtenido junto con los
grados, quedando nuestra conversion de la siguiente manera:
25.5 = 25° 30´
sábado, 4 de octubre de 2014
RADIANES
RELACIÓN ENTRE GRADOS Y RADIANES
RADIÁN:
Es la medida de un ángulo, donde el vértice de origen se
encuentra en el punto medio de una circunferencia, cuyo arco tiene la misma
longitud que el radio.
Ejemplo:
La forma para calcular la longitud del arco de una circunferencia es:
s= rq
s= longitud del arco
r= radio
q= amplitud del ángulo
CONVERSIÓN DE GRADOS
A RADIANES
La fórmula general utilizada para la conversión de grados a
radianes o también conocido como la conversión del Sistema Sexagesimal a Sistema Cíclico
es:
Ejemplo 1
(Convertir 50° a rad):
Primero se multiplican los grados a convertir por ambos
lados de la fórmula para que se pueda representar una igualdad en la fórmula
original.
Posteriormente se realiza la multiplicación del lado
izquierdo, en este caso se multiplica 50 x 1°;por otra parte se divide el valor
de pi (π) entre 180, quedando de esta forma:
50°= (0.0174) (50) rad
Después, el resultado de la división de π entre 180 se
multiplica por los grados a convertir (50):
50°=0.87 rad
Así de esa forma se obtiene el valor de 50° en rad.
Para entender he aquí otro ejemplo…
Ejemplo 2
(Convertir 130° a rad):
Primero se multiplican los grados a convertir por ambos
lados de la fórmula para que se pueda representar una igualdad en la fórmula
original.
Posteriormente se realiza la multiplicación del lado
izquierdo, en este caso se multiplica 130 x 1°;por otra parte se divide el
valor de pi (π) entre 180, quedando de esta forma:
130°= (0.0174) (130) rad
Después, el resultado de la división de π entre 180 se
multiplica por los grados a convertir (130):
130°=2.262 rad
Así de esa forma se obtiene el valor de 130° en rad.
CONVERSIÓN DE RADIANES
A GRADOS
La fórmula general utilizada para la conversión de radianes
a grados o también conocido como la conversión del Sistema Cíclico a Sistema Sexagesimal es:
Ejemplo 1
(convertir 2π rad= ¿? Grados):
Del mismo modo que la conversión de grados a radianes,
Primero se multiplican el rad a convertir por ambos lados de la fórmula para
que se pueda representar una igualdad en la fórmula original.
Posteriormente se realiza la multiplicación del lado
izquierdo, en este caso 2π x rad; por otra parte 2π sustituye al 180 de modo
que 2π se divida entre π y el resultado se multiplique por 180, quedando de la
siguiente manera:
El resultado queda de la siguiente manera, pues π al
dividirse entre π se cancela:
2π rad = 2 (180)
Después, el 2 se multiplica con el 180, teniendo como
resultado lo siguiente:
2π rad = 360°
Ejemplo 2
(Convertir 5π rad = ¿? Grados)
Del mismo modo que la conversión de grados a radianes,
Primero se multiplican el rad a convertir por ambos lados de la fórmula para
que se pueda representar una igualdad en la fórmula original.
Posteriormente se realiza la multiplicación del lado
izquierdo, en este caso 5π x rad; por otra parte 5π sustituye al 180 de modo
que 5π se divida entre π y el resultado se multiplique por 180, quedando de la
siguiente manera:
El resultado queda de la siguiente manera, pues π al
dividirse entre π se cancela:
5π rad = 5 (180)
Después, se multiplica 5 por el 180, teniendo como
resultado:
5π rad = 900°
viernes, 3 de octubre de 2014
TRIÁNGULOS
El triángulo
Es un polígono de tres lados, determinado por
tres ángulos y tres vértices para la notación de un triángulo, se emplea el
símbolo: Δ
El triángulo Δ ABC, tiene:
1) Sus vértices se denotan por letras mayúsculas:
A, B, y C.
2) Sus lados de denotan por la misma letra del
vértice opuesto, pero en minúscula: a, b y c.
CLASIFICACIÓN DE
TRIÁNGULOS SEGÚN SUS LADOS
Se clasifican según sus lados en:
1.-Escalenos: son aquellos que tienen los tres
lados distintos
2.-Isósceles: son los que tienen dos lados iguales
y uno desigual
3.-Equilátero: son los que cuentan con los tres
lados iguales
CLASIFICACIÓN DE LOS TRIÁNGULOS SEGÚN SUS ÁNGULOS
Esta clasificación se debe a sus ángulos.
1.-Rectángulos: son aquellos que
cuentan con un anguilo recto, esto es, que mida exactamente 90°.
2.-Acutángulos: son aquellos que
tienen los tren ángulos agudos, es decir, que midan menos de 90°.
3.-Obtusángulos: son aquellos que
tiene un ángulo obtuso, esto es, que mida más de 90° pero menos de 180°.
PROPIEDADES DE LOS TRIÁNGULOS
Propiedad 1:
La suma de los tres ángulos de un triángulo es de 180°.
Esto es: A+B+C=180°
Propiedad 2 (Propiedad Triangular):
Cada lado debe ser menor que la suma que los otros dos
lados.
Esto es: 5+5 =10 y si sumamos cualquier otro lado siempre nos va a dar un resultado mayor que el lado cualquiera sobrante
Propiedad 3:
1) El triángulo equilátero tiene tres ángulos
iguales, es decir, cada uno mide 60° así su suma será de 180°, respetando la
primera propiedad.
2)En el triángulo rectángulo, el lado opuesto
al ángulo recto se le denomina hipotenusa y los lados que componen al ángulo
recto se denominan, catetos.
3)Un triángulo rectángulo isósceles tiene un
ángulo recto, por lo tanto los otros dos ángulos miden lo mismo, es decir 45°.
jueves, 2 de octubre de 2014
RECTAS Y PUNTOS NOTABLES EN EL TRIÁNGULO
MEDIATRIZ
Recta perpendicular trazada desde
el punto medio da cada lado del triángulo a su
prolongación, es decir, su lado opuesto; se cortan en un punto llamado
circuncetro, que es el centro de la circunferencia del triángulo.
BISECTRIZ
Es la recta que parte de cada
vértice del triángulo y divide a los ángulos en dos iguales; se cortan en un
punto llamado incentro, que es el centro de la circunferencia inscrita en el
triángulo.
MEDIANA
Recta trazada desde un vértice hasta el punto medio del lado opuesto a
este; se cortan en un punto llamado baricentro, el baricentro es la gravedad
del triángulo, es decir, el punto de equilibrio.
ALTURAS
Es la recta perpendicular trazada
desde un vértice a su prolongación, es decir, su lado opuesto; se cortan en un
punto llamado ortocentro.
RECTA DE EULER
La recta de Euler contiene los puntos llamados, circuncentro, baricentro
y ortocentro en un mismo triangulo.
miércoles, 1 de octubre de 2014
POLÍGONOS SEMEJANTES
Dos triángulos son semejantes si tienen la misma forma pero no el mismo
tamaño, para indicar que dos triángulos son semejantes se utiliza el símbolo~.
Donde el símbolo ~ se lee "es semejante"
Ejemplo:
Para indicar que dos triángulos son semejantes se expresa de la siguiente manera:
ΔABC~ΔA´B´C´
PROPIEDADES FUNDAMENTALES DE LOS TRIÁNGULOS
SEMEJANTES
Propiedad I:
Dos triángulos son semejantes si sus ángulos correspondientes son
iguales, ejemplo:
ΔABC~ΔA´B´C´
porque los ángulos son los siguientes:
ÐA=ÐA´
ÐB=ÐB´
ÐC=ÐC´
Ejemplo:
Propiedad II:
Dos triángulos son semejantes si la razón (comparación entre dos lados) es proporcional.
Ejemplo:
TEOREMAS DE SEMEJANZA DE TRIÁNGULOS
Teorema I:
Dos triángulos son semejantes si tienen dos ángulos homólogos, es decir
iguales, en este caso el teorema solo requiere dos ángulos mientras que la
propiedad menciona todos.
Ejemplo:
Si <C=<C´ y <A=A´, entonces, el Δ ABC~ Δ A´B´C´
Teorema II:
Dos triángulos son semejantes si sus tres lados son proporcionales, en
este caso el teorema menciona los tres lados mientras que la propiedad solo
requiere la razón, lo que quiere decir que es la comparación entre dos lados
del triángulo.
Ejemplo:
por lo tanto Δ ABC~ Δ A´B´C´
Teorema III:
Dos triángulos son semejantes si
tienen un ángulo igual y los lados que forman dicho ángulo son proporcionales.
Ejemplo:
Si <K=<K´ y  entonces Δ ABC~ Δ A´B´C´
entonces Δ ABC~ Δ A´B´C´
martes, 30 de septiembre de 2014
POLÍGONOS CONGRUENTES
Polígonos Congruentes
Los triángulos o polígonos congruentes
son aquellos que tienen la misma forma y tamaño, por lo tanto para que
sean congruente se requiere los dos aspectos siguientes:
1) Sus lados son homólogos, es decir iguales.
2) Sus ángulos son homólogos, es decir iguales.
Para representar que los triángulos son congruentes se requiere el símbolo@.
Donde el símbolo = representa
la longitud, es decir, los lados.
Y donde el símbolo~representa
la amplitud, es decir, los ángulos; cabe mencionar que este símbolo se
ocupa para los triángulos semejantes.
Ejemplo:
POSTULADOS DE CONGRUENCIA DE
Postulado I: Lado, Lado,
Lado ( L,L,L)
Dos triángulos son
congruentes si sus lados son iguales
Ejemplo:
Postulado II: Ángulo,
Lado, Ángulo (A,L,A)
Dos triángulos son
congruentes si tienen dos ángulos y el lado adyacente (que los une) son
respectivamente iguales.
Ejemplo:
Postulado III: Lado,
Ángulo, Lado ( L,A,L)
Dos triángulos son
congruentes si dos lados y el ángulo formado por estos son respectivamente
iguales.
Ejemplo:
lunes, 29 de septiembre de 2014
TEOREMA DE PITÁGORAS
TEOREMA DE PITÁGORAS
El teorema de Pitágoras se utiliza para resolver triángulos
con respecto a sus lados.
Resolver un triángulo: En
trigonometría se refiere a conocer los
tres lados y tres ángulos de un triángulo
rectángulo, por medio de métodos analíticos.
Para resolver un triángulo
con respecto sus lados es necesario utilizar un triángulo rectángulo.
TRIÁNGULO RECTÁNGULO
Es aquel triangulo cuyo uno de sus ángulos es recto (90°), mencionando que el lado opuesto a dicho ángulo
se llama hipotenusa y los lados restantes se llaman catetos.
Ejemplo:(triangulo
rectángulo)
El
teorema de Pitágoras nos dice: c2= a2 + b2; es
decir el cuadrado construido sobre la
hipotenusa es igual a la suma de los cuadrados construidos sobre los catetos.
Ejemplo:
Dónde:
a=4, b=5 y c=6.
Ejemplo 1:
Calcular
el valor de la hipotenusa desconocida con los catetos dados:
a=
5 b=12 c=___________
Donde
el 5 se eleva al cuadrado al igual que
el 12.
a=
(5)2 b= (12)2
a=
25 b=144
Si c2= a2 + b2 entonces:
c2=
25 + 144
c2=
169
c= raíz cuadrada de 169 que nos da como resultado que:
c=13
Ejemplo
2:
Dado
el valor de la hipotenusa, calcular el valor del cateto no dado.
b=
7 c=25 a=_________
En este
caso la formula general del teorema de Pitágoras cambia:
c2=
a2 + b2
Quedando
así:
c2
– b2= a2
Entonces
el 25 se eleva al cuadrado menos el cuadrado del 7.
a2=
(25)2- (7)2
a2=625-49
a2=576
a=24
Suscribirse a:
Comentarios (Atom)