VALORES EXACTOS DE LAS RAZONES TRIGONOMÉTRICAS DE LOS ÁNGULOS DE 30°, 45° Y 60°

VALORES DE 30° Y 60°

Los pasos para sacar por método gráfico los valores exactos de 30° y 60°, son los siguientes:

          a)    Formar un triángulo equilátero con longitud de 2cm en cada lado.

donde a es = 2cm

          b)    Dividirlo en dos partes iguales, a partir del punto medio de la base hasta el vértice opuesto (se forman dos triángulos rectángulos)

          c)    Tomar uno solo de los dos triángulos que se formaron, con la longitud  que le corresponde.

          d)    Con el teorema de Pitágoras localizar la altura del triángulo rectángulo que se forma 

         A²+B²=C²

    C²-B²=A²

    2²-1²=A²

      4-1= A²

Obteniendo así que la altura del triángulo es la raíz cuadrada de 3 como se muestra en la siguiente figura

 e)    Seleccionar un Angulo diferente (¹) al recto (90°), para determinar las razones trigonométricas.

   *seno, coseno y tangente de el ángulo de 30° de acuerdo al angulo se le da nombre a cada uno de los lados, teniendo que el lado con valor 1 es el cateto opuesto (co), el lado de valor 2 es la hipotenusa (hip), y el lado de valor raíz cuadrada de 3 es el cateto adyacente (ca)

por lo tanto:

         Sen30°=  co   

                          hip

         Sen30°=  1  

                         2

             Así es como sabemos que el valor de seno para el angulo de 30° es:   1   

                                                                                                                              2

     Lo mismo se hace para conocer el valor de coseno y tangente de 30°; y para el ángulo de 60° se repite el procedimiento, pero ahora los nombres que reciben se dan respecto del ángulo de 60°, en la siguiente imagen se muestran ya los valores de seno, coseno y tangente para los ángulos de 30° y 60°

       

Recordemos que:

   Sen x=  co                             Cos x=   ca                       Tan x=  ca  

                hip                                         hip                                     co

    

En este caso x= 30° y 60°

VALORES EXACTOS DE 45°

Los pasos para sacar por método gráfico los valores exactos de 45°, son los siguientes:

           a)    Formar un cuadrado con valor de 1 por cada lado.

Donde a y b son iguales  a 1

           b)    Trazar una diagonal (/) de vértice a vértice. La diagonal no debe ser inversa.

           c)    Seleccionas uno de los triángulos; se recomienda el del lado derecho, y se determina su longitud (valores).

    

          d)    Por medio del teorema de teorema de Pitágoras conocemos la hipotenusa, es decir el valor faltante.

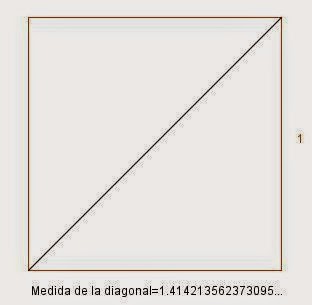
   c²=a²+b²

c²=1²+1²

c²= 1+1

obteniendo que:  c²    es = raíz cuadrada de 2, como se muestra en la siguiente figura

      e)    Seleccionar cualquier de los dos ángulos diferentes al recto (90°) y determinar las razones trigonométricas.

 Tan45°=   co  

                  ca

Sen45°=   1    = 1

                            1

     Así es como obtenemos el valor exacto de tangente para el ángulo de 45°; y el mismo procedimiento se realiza para seno y coseno de 45°, a continuación se muestra una imagen con los valores exactos ya expresados:

Como dato, se deja aquí abajo una tabla con los valores exactos de las razones trigonométricas: seno, coseno, tangente de los ángulos notables: